توی این پست می خوام تعریف کنم اصلا مشتق و انتگرال چی هستن و به زبان ساده مفهوم انتگرال و مشتق رو تعریف کنم.
همه توی دبیرستان و دانشگاه زیاد مشتق و انتگرال خوندیم که با استفاده از فرمول های خاص، جواب رو بدست میاریم. اصلا کاری به حل معادلات دیفرانسیل و انتگرال ندارم. توی این پست می خوام مفهوم اینها رو بگم و بپردازم.
توی درسهای مهندسی و تخصصی مون خب خیلی لازم میشد از مشتق و انتگرال استفاده کنیم. ولی فقط حفظی استفاده می کردیم. هیچ موقع نمی دونستیم که چرا این مشتق استفاده میشه و اونجا انتگرال. اصلا نمی دونستیم که اینها چی هستند. فقط صرفا از روی حفظ و بر اساس دستوری که استاد بهمون داده بود انجام می دادیم!
لازم به ذکره چون عکسها انگلیسی هستند بهتره ترجمه مشتق و انتگرال به زبان انگلیسی رو بدونید:
مشتق به انگلیسی میشه (derivative) و انتگرال میشه (integral).
فعل مشتق گرفتن میشه (differentiate) و فعل انتگرال گرفتن میشه (integral).
مفهوم مشتق
اساسا مشتق رو میشه به عنوان شیب منحنی یک تابع ریاضی معرفی کرد.
اما اثراتش برای مدل سازی طبعیت بسیار عمیق تر از این می رود. اهمیت مشتق در این واقعیت است که بسیاری از کمیت های فیزیکی مثل سرعت، شتاب، نیرو و غیره به عنوان نرخ های بلافاصله تغییر کمیتهای دیگر تعریف می شوند. مشتق به شما مقدار دقیقی برای آن نرخ تغییر می دهد و منجر به مدل سازی دقیق کمیت مطلوب می شود.
مفهوم انتگرال
انتگرال را می توان به عنوان ناحیه (مساحت) زیر منحنی یک تابع ریاضی معرفی کرد.
انتگرال به شما روشی ریاضی برای رسم تعداد نامحدود بلوک و بدست آوردن عبارت تحلیلی دقیق برای آن ناحیه می دهد. این برای علوم فیزیک خیلی مهم است جاهایی که تعاریف بسیاری از کمیتهای فیزیکی می توانند به شکلی ریاضی مانند ناحیه ای زیر منحنی نشان داده شود.
ناحیه یک بلوک کوچک زیر منحنی را می توان به عنوان عرض طنابی ضرب در (وزنی) ارتفاع طناب در نظر گرفت. بسیاری از مجموعه های پیوسته وابسته به جمع های وزنی هستند.
عکسهای مفهومی
در زیر سعی می کنم با عکس و تصویر، مفهوم مشتق و انتگرال رو نشون بدم:
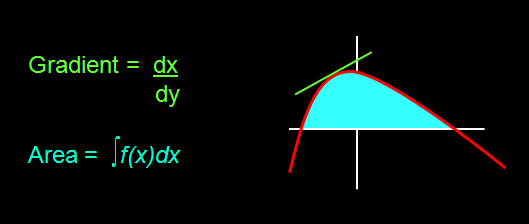
عکس بالا، طبق تعریف مون نشون میده که مشتق یعنی اندازه گیری شیب یه منحنی (تصویر چپ) که با خط قرمز نشون داده شده. عکس سمت راست هم انتگرال رو نشون میده که ناحیه (یا مساحت) زیر یک منحنی رو حساب می کنه که با کادر قرمز نشون داده شده.
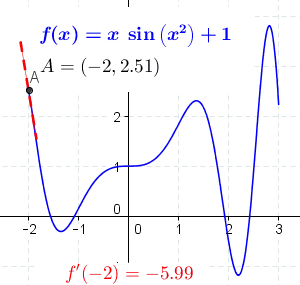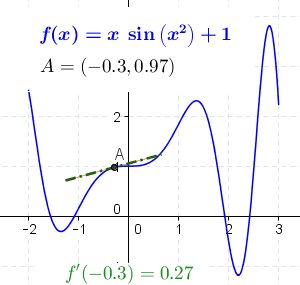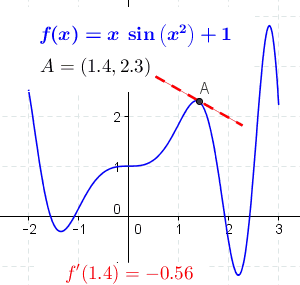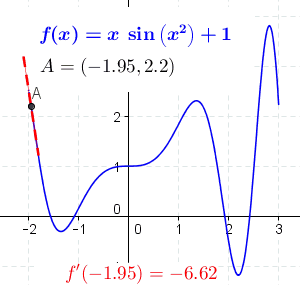
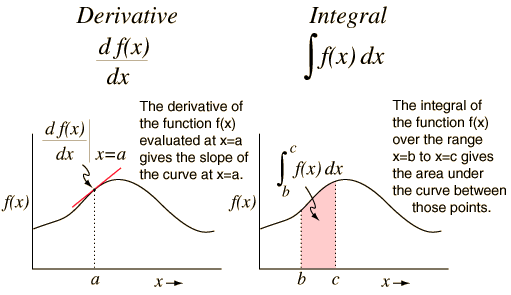
تصویر بالا خیلی جالبه. به صورت کاملا واضح مفهوم مشتق رو نشون میده. اون خط متحرک A در هر نقطه ای که قرار می گیره شیب (یا همان مشتق) منحنی در آن نقطه رو محاسبه می کنه.
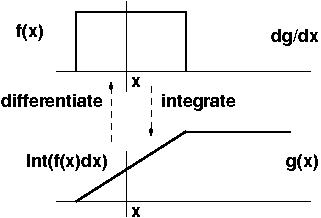
عکس بالا هم خیلی جالب نشون میده. ولی راستش من کامل متوجهش نشدم.
سوالی داشتید توی کامنت بپرسید.